All right, math wizards, here’s a trick question: does a circle have more than 360° in it?
The answer: nope. Once you go all the way around a circle, you end up back at the beginning! Pretty easy, right?
But that doesn’t mean an angle can’t have more than 360°. Here’s an example:
Say we’re on a Ferris Wheel. If the ride’s any good at all, you just don’t make one trip around and then get off. You keep on going for several rounds, right? For each revolution, we make repeated trips and the degrees we travel doesn’t just start over at 0.
We end up with a graph that looks like this:
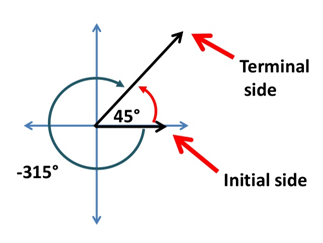
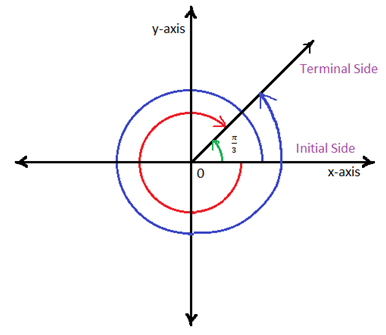
So what does that have to do with coterminal angles? It’s pretty easy once we think about it. Say we traveled 45° on the initial go around.
Where we started is the Initial side of the angle. Where we stopped is the terminal side of the angle. Neat, huh?
If we were going in the opposite direction of the initial side, we would be going in a negative direction. In this case, starting at the initial side and going “backwards” to the terminal side gives us -315°. When we make a complete loop, degrees traveled will be 360° and the negative angle will be 0°. If this doesn’t make sense, it might be a good idea to get some math homework help.
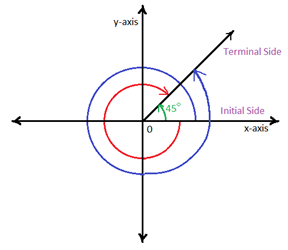
But what if we kept going after we completed the loop and landed back at the terminal side? It would look like this:
See how we traveled from in a complete loop from the terminal side?
To find out how many degrees we traveled in, simply add 360° to the initial angle!
45°+360°=405°
We can say that 45° and 405° are coterminal.
But we can also do more! Coterminals can be negative as well. Remember the -315° from going backwards? That angle also shares the same initial and terminal sides.
Thus, 45°,-315°,and 405° are all coterminals!
*****BASIC RULE: just add or subtract 360° to your initial angle and you can find a coterminal. The possibilities are endless! Take a look below:
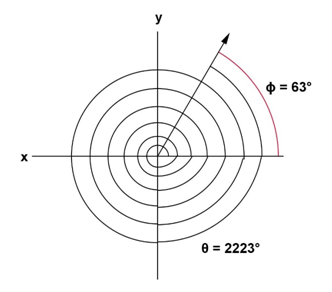
63° and 2223° are coterminals. And we can keep going!
How else can we measure coterminals? Well, we don’t have to use degrees. We can use radians.
What’s a radian?
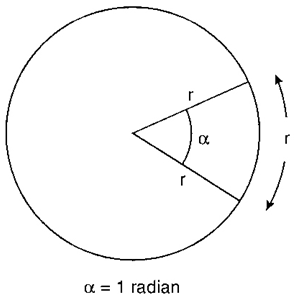
A radian is the measurement of an angle in a circle where the radius is the same as the angle’s arc.
Here’s a radian:
How many radians are in a circle? Well, the formula we use is: there are 2π radians in a complete circle. We divide it like so:
Have a circle is π, and a complete circle would bring us back to 2π.
How much is 2π?
We know that π=3.14159….and then goes on forever and ever and ever.
That makes 2π=6.28318
Since there are 2π in a complete circle, that means there are 6.28318 radians in a circle.
That means that 6.28318 radians=360°
One rad is 57.296°!
Awesomely Rad, I know!
The same principle applies to radians as they do degrees.
If we need to find a coterminalangle, we can add or subtract 2π!
It’s as easy as that.
Quick example: we have an angle with radian π/3. What is the coterminal angle?
Just add 2π!
π/3+2π→ 2π/6+12π/6→14π/6→7π/3 radians
If we want to find more coterminal angles, we can add or subtract 2π! The possibilities are endless!
Did you want to convert this measurement to degrees?
7π/3 × (360°)/2π→7/1×120/2→7×60=420°
Here are the basic formulas:
For coterminals of degrees -> add or subtract 360°
For coterminals of radians -> add or subtract 2π
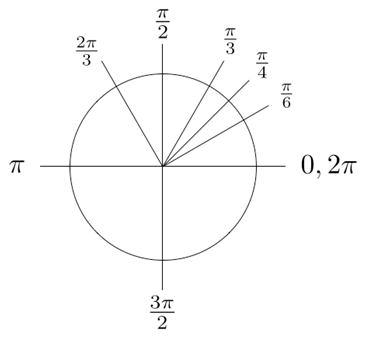
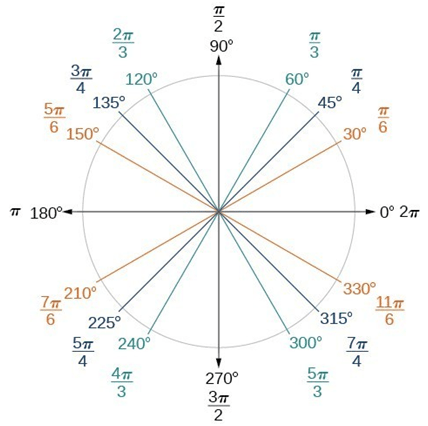
Here’s a quick cheat sheet conversion chart from radians to angles:
Congrats! You are now a radical coterminal angle wizard! Move forward to learn the half angle formula.