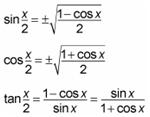The half-angle formula, and its counterpart, the double-angle formula, will usually crop up in trigonometry, and sometimes pre-calculus classes. Sometimes you’ll be instructed to evaluate a trig function of an angle that’s not specifically included on the unit circle, and by using the identity of an angle that is included, you can still evaluate the function. For example, if you’re asked to find sin105º, an angle that’s not on the unit circle, you can use a half-angle identity and substitute 210º, which is on the unit circle, for 105º. The half-angle formulas for sine, cosine, and tangent are as written:
Follow this step-by-step process to use the half angle formula successfully or connect with a trigonometry tutor to get some math homework help.
If we’re trying to find sin105º, we first have to recognize that 105º is half of 210º, which is featured on the unit circle. We’d then rewrite the function as sin(210/2). Notice that the sine equation has the ± symbol, so we need to determine whether this function will be positive or negative. 105º lies in the second quadrant of the unit circle, so it will be positive. We then substitute x for the full angle value of 210. We then look to the unit circle again to find the cosine value of 210º, which is -3/2, and substitute that value for cos210. The final step is to simplify the function if possible. In this case, we can, because the denominators can be simplified.
While the formula seems tricky at first, it can be incredibly helpful in evaluating angle functions that are not listed on the unit circle. Always remember to be mindful of your plus and minus signs, as a function can transform into something completely bizarre and unintended otherwise. It also pays to check your simple addition, subtraction, and multiplication; mastering the formula isn’t worth much if you mix up your simple equation procedures. With the right amount of practice, the possibilities are limitless! StudyGate provides online learning resources to attain academic excellence.