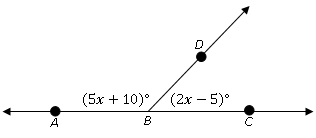Okay, here’s a brain zinger: if someone tells you that they are using the awesome Angle Addition Postulate, what do you think they are adding?
If you said “angles,” you would be 100 percent correct!
The Angle Addition Postulate basically means we are taking two angles and joining them together to make one LARGER angle!
Here’s a basic example”
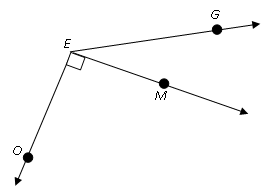
We’ll take ∠GEM and ∠MEO
- Let’s join them together do that the angle converges at point E.
- We’ll also lay them together so that the two angles share the same border EM.
What can we do with the Angle Addition Postulate?
Great question!
Let’s look at the above angle again. If ∠GEO was 125°, then what is ∠GEM?
Even without geometry help from an online math tutor, it’s almost like slicing a piece of cake!
∠GEM + ∠MEO = ∠GEO
∠GEM + ∠MEO = 125°
We know that ∠MEO = 90° because it is a right angle with the little square.
∠GEM+ ∠90° = 125°
∠GEM = 35°
Let’s go for something harder:
What are the angles below?
Easy!
First of all, we know that ∠ABD and ∠DBC follow the Angle Addition Postulate. This is because they share the same vertex at point B. The two angles share the same line BD, so they line up.
∠ABD + ∠DBC = ∠ABC
We know that AC is a straight line, and straight angles are 180°
We also have the formulas for ∠ABD and ∠DBC
Let’s plug ‘em in:
∠ABD + ∠DBC = ∠ABC
(5x+10) + (2x-5) = 180°
5x + 10 + 2x – 5 = 180
7x + 5 = 180
7x = 175
x = 25
So, now that we know what is, we can plug it into the original formulas! ∠ABD = 5x + 10, x = 25
∠ABD=135°
∠DBC = 2x – 5, x = 25
∠ABD=45°
Let’s check:
∠ABD + ∠DBC = ∠ABC
We are balanced!
For more on how to use the half-angle formula.