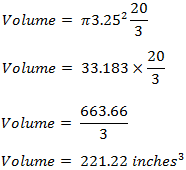Poor little Jack Horner
Sat in a class corner
With a cone on his head.
His teacher poked the cap.
“What’s the volume? Don’t nap!”
Let’s give Jack a helping hand!
First of all, let’s define the term. A cone is pretty cool, even if Jack doesn’t think so. It’s a shape with a circular base that tapers off to a point at the apex. Cones are everywhere—you see ‘em on busted roads, you can use ‘em as a funnel when pouring liquids, and my favorite—you can pack ice cream in ‘em!
But to get back to Jack. Here’s the formula to calculate the volume of a cone:
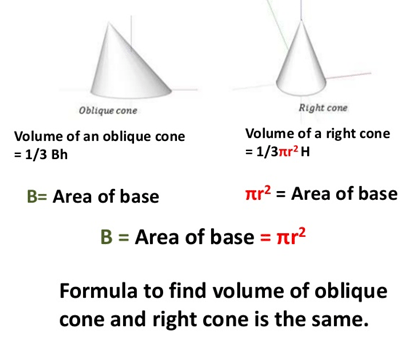
***Super neat trick in case the teacher throws a slanted dunce cap at Jack: it does not matter if the cone’s apex is not directly above the circle’s center. The slant does not need to be the same length.
 Now, let’s get Jack out of the corner pronto!
Now, let’s get Jack out of the corner pronto!
A cone’s formula is actually very simple, and we can explain it further if you want to get some equations homework help. The most complicated part is the first part of the equation. It might look familiar. It is the formula for an area of a circle.
This makes sense since the bottom of the cone is a circle! We want to find out how much space is contained within.
After that, we just need to calculate the cone’s depth by taking the height (as if it were a cylinder—see my blog on calculating the volume of a cylinder—and dividing the height by 3).
Let’s get some numbers.
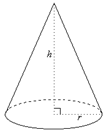
We’ll say that Jack’s cap is 6.5 inches in diameter and a height of 20 inches (yeah, the teacher loves dramatics!)
Okay, this isn’t too bad. The first thing we need to do is calculate the circular area.
We have the diameter, but we need the radius. This is easy. The diameter is the length of half the circle. The radius is the distance between the circle’s center to the edge.
Okay! Now just plug in the numbers to calculate the volume of the cone!
(We could also just plug in the radius here, but we already know what the area is!) If this is confusing, it would help to message an equations tutor.
Don’t forget the small 3 since we are dealing with three dimensions for volume!
So Little Jack Horner
leaped from his corner
Having aced his question.
Oh, but for the poor boy, alas!
For running in class,
He was sent back at Teacher’s discretion.
This time, Jack’s on his own. But at least he has the skills to figure this one out!